GAT
Contents
GAT#
\(\def\bm{\boldsymbol}\)GATは隣接する節点の中でも重要なものと重要ではないものがいるという考えのもと,どれが重要なのかも学習するGraph neural networkです.基本的な部分はGCNと大きな差はありません.
GATの理論#
GATでは隣接節点からの特徴量を集約する際に重要度\(\alpha\)(アテンション)を掛けます.
\(\bm{H}_v^{(l+1)}=\sigma(\sum_{u \in \mathbb{N}_v\cup v}\alpha_{vu} \bm{H}_u \bm{W}^{(l)})\)
\(\alpha_{vu}\)がどういう計算になるかというと,
\(\alpha_{vu}=\frac{exp(LeakyReLU(\bm{a}(\bm{W}\bm{H}_v||\bm{W}\bm{H}_u)))}{exp(\sum_{m\in \mathbb{N}_v}LeakyReLU(\bm{a}(\bm{W}\bm{H}_v||\bm{W}\bm{H}_m)))}\)
となります.
ポイントは\(LeakyReLU(\bm{a}(\bm{W}\bm{H}_v||\bm{W}\bm{H}_u))\)部分です.分子と分母がややこしいですが,ソフトマックス関数を用いて,節点\(v\)にとっての節点\(u\)の重要度を[0,1]にしているだけです.
\(LeakyReLU(\bm{a}(\bm{W}\bm{H}_v||\bm{W}\bm{H}_u))\)を解説すると,\(\bm{a}\)はベクトルをスカラーに変更する学習パラメータで,\(\bm{H}_v\)と\(\bm{H}_u\)を学習パラメータ\(\bm{W}\)により線形変換しています.これにより,よしなに節点の重要度を学習します.
さらに,GATでは複数のアテンションを用いるマルチヘッドアテンションが採用されています.
\(\bm{H}_v^{(l+1)}=||_{k=1}^K\sigma(\sum_{u \in \mathbb{N}_v\cup v}\alpha_{vu} \bm{H}_u \bm{W}^{(l)})\)
これにより,複数種類の重要度を学習することを狙っています. 一点注意点として,\(K\)個の特徴量を結合しているためl+1番目の層の特徴量のサイズが大きくなります.
GATのイメージは周りからembeddingを集める際に強弱をつけるということになります.この強弱の付け方も合わせて学習することができます.
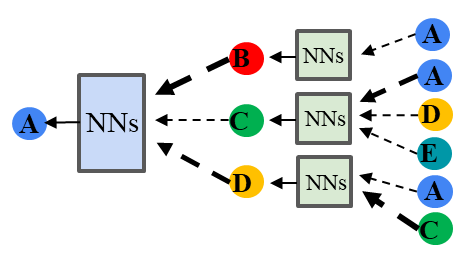
GATの実装#
GAT層の実装例は以下となります.ポイントは,attentionの作成になります.
class GraphAttentionLayer(nn.Module):
def __init__(self, in_features, out_features, dropout, alpha, final=False):
super(GraphAttentionLayer, self).__init__()
self.dropout = dropout
self.in_features = in_features
self.out_features = out_features
self.alpha = alpha
self.final = final
self.W = nn.Parameter(torch.empty(size=(in_features, out_features)))
nn.init.xavier_uniform_(self.W.data, gain=1.414) # Xavierの方法により初期化.どんな方法でもよい
self.a = nn.Parameter(torch.empty(size=(2*out_features, 1)))
nn.init.xavier_uniform_(self.a.data, gain=1.414) # Xavierの方法により初期化.どんな方法でもよい
self.leakyrelu = nn.LeakyReLU(self.alpha) # Attention計算用のLeakyReLu関数
def forward(self, h, adj): #hはNNへの入力行列
Wh = torch.mm(h, self.W)
e = self._prepare_attentional_mechanism_input(Wh)
zero_vec = -9e15*torch.ones_like(e)
attention = torch.where(adj > 0, e, zero_vec) # 枝がないところは attentionを0にする
attention = F.softmax(attention, dim=1) # dim=1は行単位でのsoftmax
attention = F.dropout(attention, self.dropout, training=self.training)
h_prime = torch.matmul(attention, Wh) # attentionの値を掛けた値の和を出力にする
if self.final:
return h_prime #最終層の場合, 活性化関数無し
else:
return F.elu(h_prime) #最終層以外は活性化関数 elu
def _prepare_attentional_mechanism_input(self, Wh):
Wh1 = torch.matmul(Wh, self.a[:self.out_features, :]) #左側 (N,1)次元行列
Wh2 = torch.matmul(Wh, self.a[self.out_features:, :]) #右側 (N,1)次元行列
#print(Wh1)
#print(Wh2)
e = Wh1 + Wh2.T # broadcast add. (N,N)次元行列. 全ての節点ペアのeを計算
#print(e)
return self.leakyrelu(e)
下記は2層からなるGATになります. GATではmulti headを採用するため,headの数だけ層を追加しています.fowardではそれぞれの層の出力をconcatして最終層に渡しています.
class GAT(nn.Module):
def __init__(self, nfeat, nhid, nclass, dropout, alpha, nheads):
super(GAT, self).__init__()
self.dropout = dropout
self.attentions = [GraphAttentionLayer(nfeat, nhid, dropout=dropout, alpha=alpha, final=False) for _ in range(nheads)]
for i, attention in enumerate(self.attentions):
self.add_module('attention_{}'.format(i), attention) #layerを定義
self.out_att = GraphAttentionLayer(nhid * nheads, nclass, dropout=dropout, alpha=alpha, final=True)
def forward(self, x, adj):
x = F.dropout(x, self.dropout, training=self.training)
x = torch.cat([att(x, adj) for att in self.attentions], dim=1)
x = F.dropout(x, self.dropout, training=self.training)
x = self.out_att(x, adj)
return F.log_softmax(x, dim=1)
GATのポイント#
周囲の節点の特徴量の重要度(アテンション)を学習することで,一様な集約ではない特徴量の集約を可能とする.
GATの文献#
Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, Yoshua Bengio, "Graph Attention Networks", ICLR 2018 https://arxiv.org/abs/1609.02907